I’ve investigated this and up to now all examples, tutorials, and so on. They at all times use the next order: scale * rotate *, however for some cause this order should at all times be the opposite means round within the graph of my scene. I’m not certain if that is meant as a result of transformation of the native matrix into World Matrix or is an error inherent in my utility.
Right here is the implementation of my easy scene chart. I’m utilizing the Vulkan and GLM Arithmetic Library.
void SceneNode::setTransform(glm::mat4 remodel) {
transformLocal = remodel;
}
void SceneNode::replace() {
// if root node
if (parentNode == nullptr) {
transformWorld = transformLocal;
} else {
transformWorld = parent->transformWorld * transformLocal;
}
for (auto &node : kids) {
node->replace();
}
}
And my shadowing logic:
// initialization code hidden for simplicity
void primary() {
// worldTransform = remodel matrix calculated throughout scene node replace
gl_Position = UniformCameraData.projectionView * ModelPushConstants.worldTransform * vec4(vPosition, 1.0f);
outColor = vColor;
}
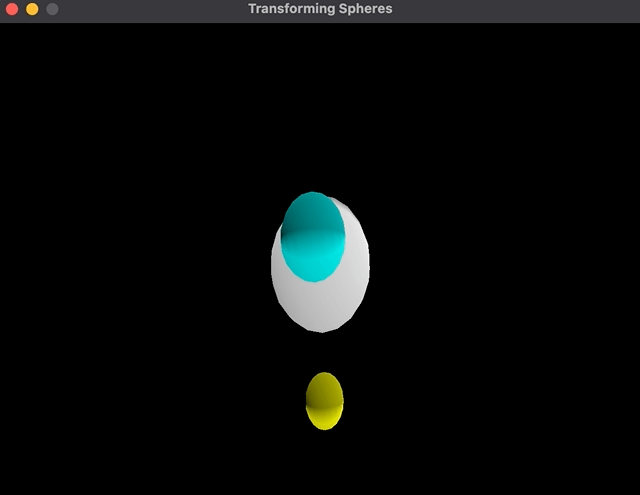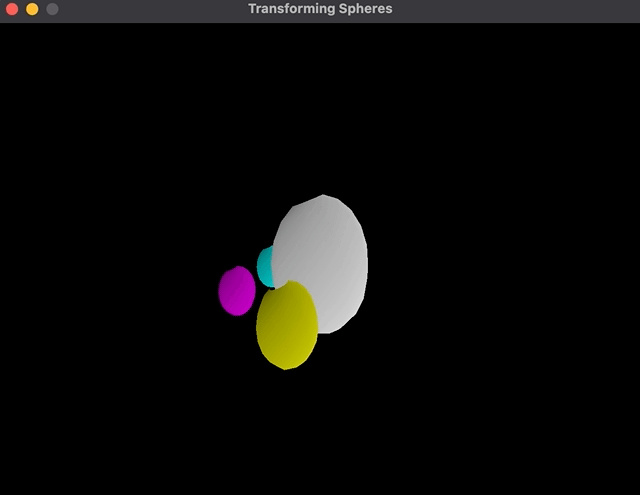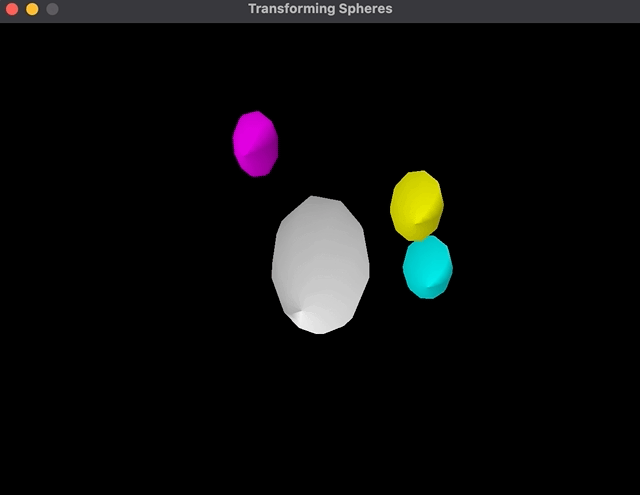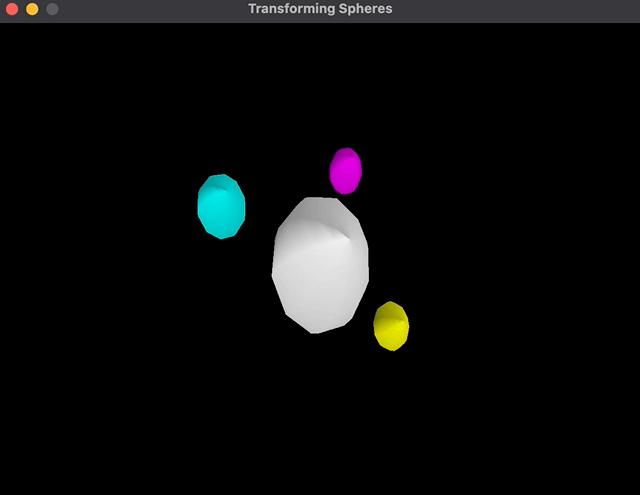
As an indication, I’ve created a brilliant easy scene with spheres:
Root
Sphere Middle -> Rotate round its personal axis
Sphere 1 -> Place someplace close to the guardian and Rotate round its personal axis
Sphere 2 -> Place someplace close to the guardian andRotate round its personal axis
Sphere 2 -> Place someplace close to the guardian andRotate round its personal axis
This scene chart offers me a sphere within the setting that rotates and three spheres that flip because of being kids of this sphere; As well as, the spheres themselves revolve round their very own axis:
Nonetheless, the implementation is unusual to me. The order of transformations is the * rotation scale * as an alternative of the opposite aspect:
child1->setTransform(
glm::translate(glm::mat4{1.0}, glm::vec3{2.0, 0.0, 0.0}) *
glm::rotate(glm::mat4{1.0f}, glm::radians(body * 0.9f),
glm::vec3{0.0, 0.0, -1.0}) *
glm::scale(glm::mat4{1.0}, glm::vec3{0.4, 0.4, 0.4}));
// ...different kids transformations
scene->replace();
When altering the order of transformations, rotation happens across the central sphere:
child1->setTransform(
glm::rotate(glm::mat4{1.0f}, glm::radians(body * 0.9f),
glm::vec3{0.0, 0.0, -1.0}) *
glm::translate(glm::mat4{1.0}, glm::vec3{2.0, 0.0, 0.0}) *
glm::scale(glm::mat4{1.0}, glm::vec3{0.4, 0.4, 0.4}));
// ...different kids transformations
scene->replace();
As you may see, the cyan shade sphere revolves across the father as an alternative of its personal heart.
I used to be confused by this, so I added the interpretation into the foundation node (for instance (2.0, 1.0)) and obtained the identical consequence. If I flip the sphere, then translate, it is going to flip towards (0, 0), then it is going to translate to (2.0, 1.0) on the identical time, which can imply that it’s in (2.0, 1.0) and turning towards (0.0, 0.0). However, if it interprets first, then I flip, it is going to flip towards (2.0, 1.0) and can translate to (2.0, 1.0) on the identical time, which can imply that it’s turning towards the newly translated heart.
Logically, this is sensible to me as a result of these multiplications are occurring on the identical time and the result’s written within the node, however I nonetheless don’t perceive why the advised transformation order is often a scale * rotate * translate. Can anybody clarify what I lack right here that I’ve to make use of multiplied transformations is in reverse order?